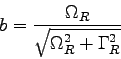Model of Diode Laser Spectra
Krishna Myneni
February 9, 2001
According to the Wiener-Khinchine Theorem, the optical
spectrum is given by the Fourier transform of the field
autocorrelation function [1]
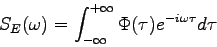 |
(1) |
The field autocorrelation function 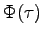 is given by
is given by
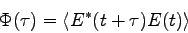 |
(2) |
where the brackets denote averaging over 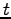 .
The time dependent
.
The time dependent 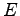 field of a laser can be expressed as
field of a laser can be expressed as
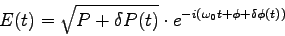 |
(3) |
where 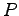 and
and 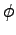 are the steady state power and initial phase
values, and
are the steady state power and initial phase
values, and 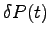 and
and
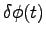 represent the
random power and phase fluctuations inside the laser. In diode
lasers spontaneous emission is the source of
represent the
random power and phase fluctuations inside the laser. In diode
lasers spontaneous emission is the source of
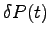 and
and
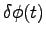 . Given suitable random
distributions for
. Given suitable random
distributions for 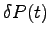 and
and
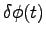 , the above
equations may be integrated numerically to evaluate the optical
spectrum
, the above
equations may be integrated numerically to evaluate the optical
spectrum 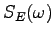 . In the simplest approximation
. In the simplest approximation
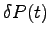 is taken to be zero, and thus
is taken to be zero, and thus
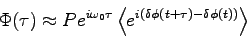 |
(4) |
The following notation will be used from hereon to simplify expressions:
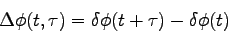 |
(5) |
Since spontaneous emission events are random, we can assume
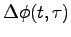 to be a Gaussian random variable. Then
it can be shown by using the result for the mean of the function
of a random variable
to be a Gaussian random variable. Then
it can be shown by using the result for the mean of the function
of a random variable 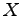 ,
,
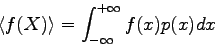 |
(6) |
where 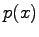 is the probability density function for
is the probability density function for 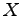 ,
that
,
that
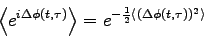 |
(7) |
and the time average
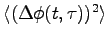 can be evaluated from a transient analysis of the laser rate
equations to a sudden change in the field intensity caused by
the spontaneous emission event. This yields the following
expression in terms of phenomenological parameters [1][2]:
can be evaluated from a transient analysis of the laser rate
equations to a sudden change in the field intensity caused by
the spontaneous emission event. This yields the following
expression in terms of phenomenological parameters [1][2]:
![\begin{displaymath}
\langle (\Delta \phi(t, \tau))^2 \rangle =
{R_{sp} \over 2...
...ta) -
e^{-\Gamma_R \tau}\cos(\Omega_R \tau - 3\delta)]\right)
\end{displaymath}](slspec-img20.png) |
(8) |
where
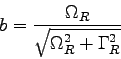 |
(9) |
and
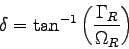 |
(10) |
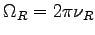 , where
, where 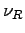 is the
relaxation oscillation frequency,
is the
relaxation oscillation frequency, 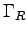 is the
damping rate of the relaxation oscillations,
is the
damping rate of the relaxation oscillations, 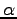 is the
linewidth enhancement factor, and
is the
linewidth enhancement factor, and 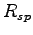 is the spontaneous
emission rate. Putting the expression for
is the spontaneous
emission rate. Putting the expression for
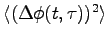 from
equation 8 into
equation 7, and substituting
the resulting expression into equation 4,
the field autocorrelation function in the approximation
from
equation 8 into
equation 7, and substituting
the resulting expression into equation 4,
the field autocorrelation function in the approximation
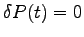 is given by
is given by
![\begin{displaymath}
\Phi(\tau) \approx
Pe^{i\omega_0 \tau}e^{-{R_{sp} \over 4P}...
...a) -
e^{-\Gamma_R \tau}\cos(\Omega_R \tau - 3\delta)]\right)}
\end{displaymath}](slspec-img29.png) |
(11) |
Equation 11 describes a
real autocorrelation function; hence, its Fourier
transform will yield a symmetric spectrum. The spectrum
is centered at frequency 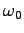 . Its central peak has a
Lorentzian profile and symmetric sidebands are present
at
. Its central peak has a
Lorentzian profile and symmetric sidebands are present
at
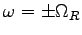 . Real diode laser spectra are
asymmetric. An analysis of the spectrum including correlated
power fluctuations was developed by van Exter,
et. al. [3].
. Real diode laser spectra are
asymmetric. An analysis of the spectrum including correlated
power fluctuations was developed by van Exter,
et. al. [3].
-
- 1
- G. P. Agrawal and N. K. Dutta, Semiconductor
Lasers, New York: Van Nostrand Reinhold, 1993.
- 2
- C. H. Henry, Theory of the phase noise and
power spectrum of a single mode injection laser, IEEE J. Quant.
Electron., QE-19, 1391.
- 3
- M. P. van Exter, W. A. Hamel, J. P. Woerdman,
and B. R. P. Zeijlmans, Spectral signature of relaxation
oscillations in semiconductor lasers, IEEE J. Quant. Electron.,
28, 1470.