A Simple Circuit Implementation
of a Van der Pol Oscillator

Ned J. Corron

            In the study of nonlinear dynamics and applied mathematics, the Van der Pol oscillator is commonly used to illustrate various phenomena including stability, Hopf bifurcation, limit cycles, and relaxation oscillations.  This mathematical model was originally developed for an electronic oscillator built using vacuum tubes; however, it is difficult today to realize this circuit in its original form due to the replacement of tubes with semiconductor technology.  Thus, it is particularly instructive to have a modern circuit implementation for demonstrating these mathematical concepts in a physical device.

            Mathematically, a general form of a Van der Pol oscillator is

                                                                                                          (1)

where e and a are constants, u(t) is the dependent state that depends on time t, and a dot denotes differentiation with respect to time.  Equivalently, the oscillator (1) can be written in system form as

                                                                                                               (2)

where  and .  This latter form is convenient for directly interpreting the response of the system in x‑y phase space.

            The oscillator (1) is widely used to demonstrate nonlinear dynamics since it is amenable to analysis.  Specifically, asymptotic techniques can be applied for the cases of both small and large e to predict the amplitude response and waveform shape.  For small e, it is a standard exercise to show that u = 0 is stable for a < 0; a Hopf bifurcation occurs at a = 0; and a stable limit cycle exists for a > 0, for which

                                                                                                                (3)

where f is an arbitrary phase.  For large e, the oscillator produces relaxation oscillations, which approach a square wave.  Numerical simulations can be used to examine the continuum that bridges these limits.

            The electronic circuit shown in Figure 1 is a Van der Pol oscillator; that is, the circuit is appropriately modeled by equation (1), or equivalently by the system (2).  The voltages V_x and V_y correspond to the states x and y, respectively.  In the circuit, the amplifiers U1, U2, and U3 are any standard operational amplifiers, such as TL082.  The devices U4 and U5 are AD633 integrated circuits, which are low cost analog multipliers with differential inputs and divide-by-ten output.  Specific component values are suggested in Table 1.

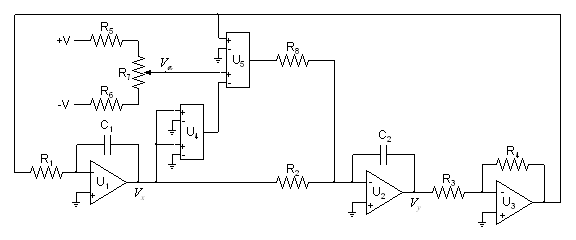
Figure 1.  Circuit for a Van der Pol oscillator.

Table 1.  Suggested component values and devices.

            For the component values suggested in Table 1, the parameter e is set to 0.1; however, other values for e can be selected by changing R₈, where

                                                               .                                                          (4)

The parameter a is set by adjusting the voltage divider at R₇, where

                                                                .                                                            (5)

Including R₅ and R₆ in the voltage divider roughly compensates for the factor of 10 in (5), thereby providing the useful range -15 < a < 15 using a ±15-volt power source.  The frequency at the Hopf bifurcation is

                                                                                       (6)

which can be adjusted by changing both C₁ and C₂ together.  In operation, the voltage V_a is monitored using a digital voltmeter, and the voltages V_x and V_y are observed with an oscilloscope.

            The interesting nonlinear dynamics of the Van der Pol oscillator can be observed by scanning V_a from negative to positive values.  In Figure 2, the system phase space trajectory observed for various V_a are shown.  These figures are screen snapshots taken from an analog oscilloscope configured in an x-y mode, with V_x and V_y connected to the x and y channels, respectively.  In a phase plane picture, a closed path represents a periodic waveform, and the special case of a sinusoidal waveform displays as a circular or elliptical path.  Deviation from an elliptical orbit indicates the presence of harmonics, and the waveform is no longer a pure sinusoid.    With a negative V_a, it is seen that the steady state V_x = V_y = 0 is observed, thus indicating it is stable.  As V_a increases toward zero, it is seen that this steady state becomes more noisy.  This is a precursor for the impending loss of stability of the steady state that will occur at the Hopf bifurcation.  As V_a is increased just past zero, a Hopf bifurcation is observed, in which a small amplitude limit cycle emerges from the steady state.  These initial oscillations are almost perfect sine waves in both x and y, seen as a circle in the phase space and the oscilloscope display.  As V_a increases from zero, the amplitude of the sinusoidal oscillations quickly grows, confirming the quadratic amplitude response in (3).  However, this rapid growth abates as V_a gets larger.  Eventually, the waveform begins to distort from sinusoidal as the nonlinear characteristics of the circuit begin to dominate.  At this point, the circuit begins to function as a relaxation oscillator, generating a waveform characterized by rapid switching between two metastable states.  In Figure 3, actual time traces of the waveforms for both V_x and V_y are shown for two positive values of V_a.  By comparing the traces in Figure 3, it is seen how the waveform deviates from sinusoidal for larger V_a.

            The response described by (3) can be confirmed experimentally using the circuit.  In Figure 4, the theoretical and observed amplitude responses for the oscillator are plotted as a function of the control parameter a.  In this figure, two observed responses are shown.  These responses are derived from the peak-to-peak voltage observed for the voltages V_x and V_y.  For small a > 0, the responses for both voltages are virtually identical and agree with that predicted in (3).  However, for larger a, the two observed responses differ significantly due to the waveform deviation from sinusoidal.  It is interesting to note that the response observed for V_x continues to track the prediction (3) even though the assumption of weak dissipation is no longer valid.

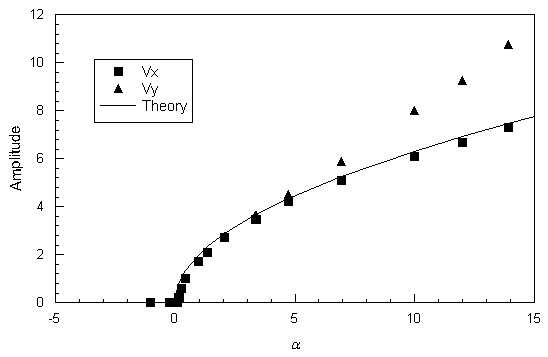
Figure 4.  Observed amplitude response for the Van der Pol circuit as a function of the control parameter a.

            In conclusion, this brief tutorial presents a modern Van der Pol circuit that is capable of showing various nonlinear phenomena including stability, Hopf bifurcation, limit cycles, and relaxation oscillations.  As a result, this simple experimental system provides a useful tool for exploring important concepts in nonlinear dynamics and serves as a starting point for further investigations in nonlinear and chaotic systems.