© 2006 Krishna Myneni
The alkali atoms are those which reside in the first column of the periodic
table. These atoms have a single valence electron in the ![]() shell,
and their quantum mechanical treatment is effectively that of a single electron
atom, e.g. the hydrogen atom. The atomic level structure of the alkali atoms,
including various internal interactions, and under external perturbations
such as static electric and magnetic fields, may then be treated
analytically. Thus, the alkali atoms have been important, historically, in the
experimental validation of the predictions of quantum mechanics. Alkali
atoms are also important from a technological standpoint. Their ground
hyperfine states, which we discuss here, are used in setting the standard for time and
frequency measurements. In addition, these states have importance in
astrophysics, since much of the information obtained from interstellar clouds
is due to radio emissions at 21 cm, emitted in transitions between hyperfine
levels of the hydrogen atom.
shell,
and their quantum mechanical treatment is effectively that of a single electron
atom, e.g. the hydrogen atom. The atomic level structure of the alkali atoms,
including various internal interactions, and under external perturbations
such as static electric and magnetic fields, may then be treated
analytically. Thus, the alkali atoms have been important, historically, in the
experimental validation of the predictions of quantum mechanics. Alkali
atoms are also important from a technological standpoint. Their ground
hyperfine states, which we discuss here, are used in setting the standard for time and
frequency measurements. In addition, these states have importance in
astrophysics, since much of the information obtained from interstellar clouds
is due to radio emissions at 21 cm, emitted in transitions between hyperfine
levels of the hydrogen atom.
In this paper we discuss how the various internal angular momenta of an
atom couple to give its total angular momentum, and the corresponding
angular momentum eigenstates of the atom. The hyperfine levels are associated
with these eigenstates. A specific example is worked out for the ground
state of the alkali atom, ![]() Rb.
Rb.
The total angular momentum of an atom consists of various parts: the
orbital angular momentum of each electron, ![]() , the intrinsic spin of each
electron,
, the intrinsic spin of each
electron, ![]() , and the intrinsic spin of the nucleus,
, and the intrinsic spin of the nucleus, ![]() , which is
actually a combined angular momentum of the nucleons, except for hydrogen.
Due to interactions inside the atom, the individual momenta are not
conserved separately -- only the total angular momentum of the atom is
conserved. The total angular momentum is given by[1]
, which is
actually a combined angular momentum of the nucleons, except for hydrogen.
Due to interactions inside the atom, the individual momenta are not
conserved separately -- only the total angular momentum of the atom is
conserved. The total angular momentum is given by[1]
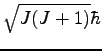 .
.
If there were no interaction between the nucleus and the electrons, other than
the Coulomb force, the set of quantum numbers
![]() for the operators
for the operators
![]() and
and ![]() , and operators for the
, and operators for the ![]() -components of
these angular momenta,
-components of
these angular momenta, ![]() and
and ![]() , would be sufficient and complete for
uniquely labeling the angular momentum states of the atom. However, the
magnetic dipole field arising from the nuclear spin exerts torque on the
electrons, coupling
, would be sufficient and complete for
uniquely labeling the angular momentum states of the atom. However, the
magnetic dipole field arising from the nuclear spin exerts torque on the
electrons, coupling ![]() and
and ![]() . Only the magnitude of the total
angular momentum
. Only the magnitude of the total
angular momentum ![]() , and its
, and its ![]() -component,
-component, ![]() , can be considered as
strictly conserved quantities. This coupling is known as the hyperfine
interaction, because it removes the degeneracy of the
, can be considered as
strictly conserved quantities. This coupling is known as the hyperfine
interaction, because it removes the degeneracy of the ![]() sub-levels and
leads to very fine structure in the spectra of atoms. Hyperfine structure in
the spectra of atoms can be observed only by very high resolution instruments
(large grating spectrometers, Fabry-Perot interferometers, or laser spectrometers).
sub-levels and
leads to very fine structure in the spectra of atoms. Hyperfine structure in
the spectra of atoms can be observed only by very high resolution instruments
(large grating spectrometers, Fabry-Perot interferometers, or laser spectrometers).
The hyperfine coupling causes the ![]() -components of
-components of ![]() and
and ![]() to not be conserved. Therefore, the quantum numbers
to not be conserved. Therefore, the quantum numbers ![]() and
and ![]() are
not ``good'' quantum numbers, i.e. the eigenstates of
are
not ``good'' quantum numbers, i.e. the eigenstates of ![]() and
and ![]() are no longer angular momentum eigenstates of the atom. The new angular
momentum eigenstates, in the presence of the hyperfine interaction, are
given by the simultaneous eigenstates of the operators
are no longer angular momentum eigenstates of the atom. The new angular
momentum eigenstates, in the presence of the hyperfine interaction, are
given by the simultaneous eigenstates of the operators ![]() and
and ![]() .
These eigenstates, which give the hyperfine levels of
the atom, are labeled by the new set of quantum numbers
.
These eigenstates, which give the hyperfine levels of
the atom, are labeled by the new set of quantum numbers ![]() . In
practice, the hyperfine interaction is very weak, and the quantum numbers
. In
practice, the hyperfine interaction is very weak, and the quantum numbers
![]() and
and ![]() are still useful to label distinct states of the atom, so the
angular momentum eigenstates are denoted by
are still useful to label distinct states of the atom, so the
angular momentum eigenstates are denoted by
![]() .
.
For given ![]() and
and ![]() , the allowed values of the quantum number for the
total angular momentum,
, the allowed values of the quantum number for the
total angular momentum, ![]() , are given by the coupling rules for two
angular momenta[2][3]:
, are given by the coupling rules for two
angular momenta[2][3]:
The angular momentum eigenstates of the atom,
![]() ,
can be written as superpositions of the uncoupled states
,
can be written as superpositions of the uncoupled states
![]() :
:
Since angular momentum conservation requires
Equations 3-5 are valid in general for any atom
in which the angular momenta are coupled as described in eq 1. Thus
far, we have not imposed any
requirements which are particular to alkali atoms. For the particular case of
the ground state of an alkali atom, only the valence ![]() -shell electron
contributes to
-shell electron
contributes to ![]() . It follows that, in this case, the quantum number
. It follows that, in this case, the quantum number
![]() is given by
is given by
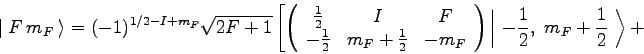
For ![]() Rb, in the ground
Rb, in the ground ![]() state,
state, ![]() and
and ![]() .
Therefore,
.
Therefore,
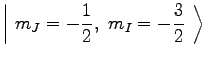 |
(7) | ||
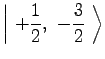 |
(8) | ||
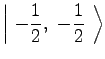 |
(9) | ||
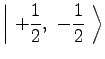 |
(10) | ||
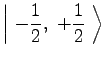 |
(11) | ||
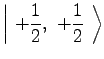 |
(12) | ||
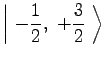 |
(13) | ||
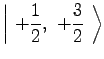 |
(14) |
Using eq 6 with ![]() , consulting a table of
, consulting a table of ![]() symbols[1], and, from eq 2, noting that the allowed
values of
symbols[1], and, from eq 2, noting that the allowed
values of ![]() are
are
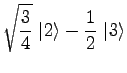 |
(15) | ||
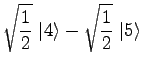 |
(16) | ||
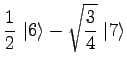 |
(17) | ||
| (18) | |||
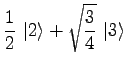 |
(19) | ||
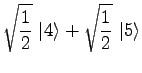 |
(20) | ||
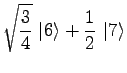 |
(21) | ||
| (22) |
For ![]() Rb, the difference in energy between the
Rb, the difference in energy between the ![]() and
and ![]() hyperfine
levels is
hyperfine
levels is
![]() , with
, with
![]() GHz[4].
The three sublevels for
GHz[4].
The three sublevels for ![]() :
: ![]() ,
, ![]() , and
, and ![]() are
degenerate, as are the five sublevels for
are
degenerate, as are the five sublevels for ![]() . The degeneracy of the
sublevels can be removed by placing the atom in an external magnetic field.
. The degeneracy of the
sublevels can be removed by placing the atom in an external magnetic field.